ALONSO E FINN VOL. 3 CAP. 10 QUESTÃO #10.5 (LETRA A)
10.5 (a) Demonstrar que la función de partición de un gas de electrones colocado en un campo magnético B es:
Porém, o momento magnético de spin é:
Assim, a energia potencial dessa interação levando em conta o campo magnético na direção Z é:
A degenerescência pode ser aproximada para 2, este valor vem da teoria quântica de Dirac. Já a projeção do spin na direção Z é:
Assim:
Podemos então catalogar a energia como duas, uma relacionada ao spin Up que tem valor positivo, e a outra ao Down que tem valor negativo:
Sabemos que a função de partição é definida como:
No nosso caso, temos:
Com algumas manipulações algébricas, chegamos em:
Multiplicando a equação acima por 2 e dividindo também por 2, temos:
Devemos lembrar que:
Então:
Nosso beta é definido como:
Então a nossa função de partição fica:
Figura 1.0: Capa do livro Alonso e Finn.
Solução:
Quando o elétron é submetido a um campo magnético, a energia potencial dessa interação pode ser escrita na forma:
Porém, o momento magnético de spin é:
Assim, a energia potencial dessa interação levando em conta o campo magnético na direção Z é:
A degenerescência pode ser aproximada para 2, este valor vem da teoria quântica de Dirac. Já a projeção do spin na direção Z é:
Assim:
Podemos então catalogar a energia como duas, uma relacionada ao spin Up que tem valor positivo, e a outra ao Down que tem valor negativo:
No nosso caso, temos:
Com algumas manipulações algébricas, chegamos em:
Multiplicando a equação acima por 2 e dividindo também por 2, temos:
Devemos lembrar que:
Então:
Nosso beta é definido como:
Então a nossa função de partição fica:










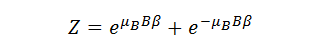





Comentários
Postar um comentário