CAMPO ELÉTRICO PRODUZIDO POR UMA LINHA DE CARGA
 |
| Figura 1.0: Anel de cargas. |
Temos como comprimento de um dos elementos de carga do anel acima, ds e λ como carga por unidade de comprimento. A carga do elemento é representada como:
O elemento cria um vetor campo elétrico dE no ponto P, que possui uma componente dEcosθ, paralela ao eixo central do anel.
A equação do campo elétrico:
Aplicando (1) em (3):
Pelo Teorema de Pitágoras encontramos o valor de r²:
Substituindo na equação (5):
Observando a figura 1.0, encontramos o valor para cosθ:
Substituindo as equações (6) e (7) em (2):
A equação acima fica na forma:
Fazendo algumas simplificações:
Integrando a extensão da circunferência do anel:
Quem varia na integração é s, então podemos escrever:
Resolvendo a integral da equação acima:
Por λ ser carga por unidade de comprimento do anel, teremos q como a carga total do anel e assim chegamos à equação de campo elétrico de um anel carregado, reescrevendo a equação acima da seguinte forma:
REFERÊNCIAS BIBLIOGRÁFICAS:



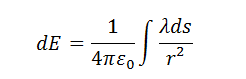









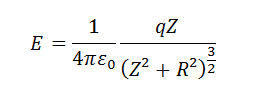
Comentários
Postar um comentário